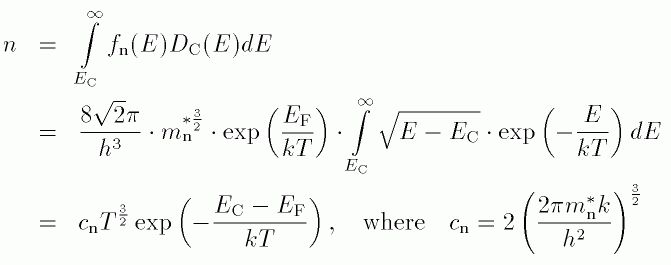
Silicon is beside germanium and some III-V semiconductors like GaAs the most important material in semiconductor industry. The fabrication of state of the art processors are impossible without silicon. The reason is that nowadays fabricated silicon single crystals are extremely clean and perfect which is an essential requirement to obtain adequate yield during silicon processing. Every chip possess a lot of active region predominantly pn-junctions. For engineering these pn-junctions the Fermi-Energy EF plays an important role in technology. The properties of a fabricated pn-junction depends strongly on the energy level of the Fermi-Energy.
In this section I will treat the temperature dependence of the Fermi-Energy.
The electron-density in the conduction-band can be calculated with the following equation:
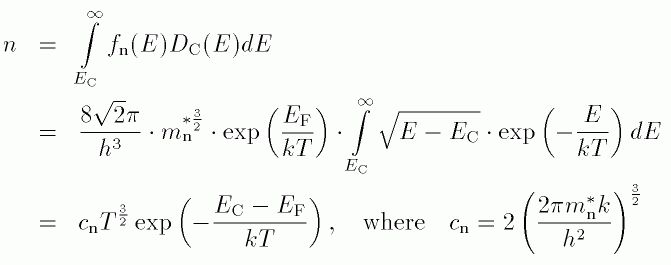
In a Similar way the hole-density in the valence-band can be calclated:
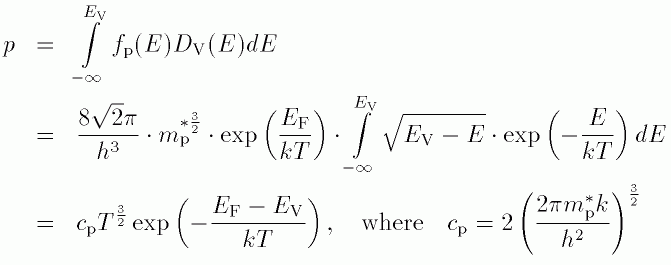
where
| EF | : | the Fermi-Energy in J | |
| fn(E) | : | the Fermi-Distribution for electrons in the conduction-band: fn(E) = {1 + exp[(E - EF)/kT]}-1 | |
| fp(E) | : | the Fermi-Distribution for holes in the valence-band: fp(E) = 1 - fn(E) | |
| DC(E) | : | the densiy of states in the conduction-band: DC(E) ~ (E - EC)0.5 | |
| DV(E) | : | the densiy of states in the valence-band: DV(E) ~ (EV - E)0.5 | |
| mn* | : | the effective mass of electrons in the conduction-band | |
| mp* | : | the effective mass of holes in the valence-band | |
| h | : | the planck-constant: h = (6.626076±4)·10-34Js | |
| k | : | the boltzmann-constant: k = (1.38066±1)·10-23J/K | |
| T | : | the absolute temperature in K | |
If the band-gap EG = EC - EV is not too narrow, then (E - EF)/kT >> 1 and the Fermi-Distribution can be replaced by the Boltzmann-Distribution: fn(E) ~ fB(E) = exp[ - (E - EC)/kT].
Let's have a look at a semiconductor containing acceptors with the concentration NA and donators with the concentration ND. At any time the condition of neutrality has to be satisfied:
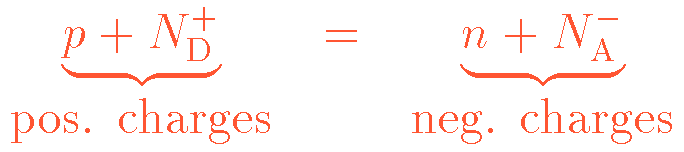
ND+ is the concentration of ionized donators and NA- is the concentration of ionized acceptors:

Insertion of the equations for ND+, NA-, p and n (see above) into the condition of neutrality yields a transcendent equation for the Fermi-Energy EF:
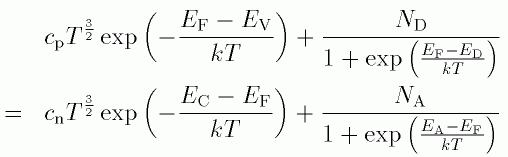 |
* |
In order to define an Error-Function Err(E) one have to bring the all terms in equation (*) to the right side and replaced zero at the left side by Err(E). Now you have to guess the right value for E. If the guessed value was wrong then Err(E) has a value unequal to zero. Only when Err(E) = 0 you have guessed the correct value and E = EF, see next figure.
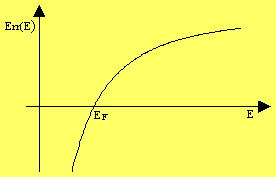 |
 |
a) Error-Function in dependence of the energy. When the Error-Function cross the E-axis then E = EF. | b) Iteration-steps to approximate the value of EF. |
In order to estimate EF you have to find the start-values EL and
ER. These value must satisfy the condition
Err(EL) · Err(ER) < 0
or in this special case Err(EL) < 0 and Err(ER) > 0. Then take
the midpoint of the interval [EL,ER]:
EM = (EL + EL)/2 and calculate
Err(EM). The sign of Err(EM) decide the selection of the
interval for the next iteration (see interval labeled "2" in the above figure):
If Err(EL) · Err(EM) < 0 then
leave EL unchanged and set ER = EM.
If Err(EL) · Err(EM) > 0 then
set EL = EM and leave ER unchanged.
Now repeat this procedure as long as the wideness of the current interval ER - EL
becomes smaller than a chosen limit. If this condition is valid then terminate the iteration procedure and set:
EF = EM.
Repeat this procedure for every temperature T.
It follows the program-structure of the above described procedure using C:
double Calculate_Fermi_Energy(double NA, double ND, double Temp)
{
double E0 E1 EF;
void Calulate_Start_Values()
{
EL = ...;
ER = ...;
}
void Interval_Nesting()
{
...
EF = ...;
}
Calculate_Start_Values;
Interval_Nesting;
return EF;
}
To see the complede program code click here .
The temperature dependence was computed for the following parameters:
| EV | = | 7.00eV | (arbitrary value) | |
| EG = EC - EV | = | 1.12eV | (silicon) | |
| EC - ED | = | 0,03eV | (donator-level) | |
| NA | = | 0 | (n-type silicon) |
The left part of the next picture shows temperarure dependance of the Fermi-Energy EF in the temperature range of 0 < T < 1500K for different donator concentrations ND. Because the melting point of silicon is TM = 1688K( = 1415°C), the chosen upper limit for the temperature is reasonable.
The right part of the picture shows the temperature dependence of the electron concentration n(T). To compute the electron concentration n, the result for EF must be inserted (for a given temperature T and donator concentration nD) in the equation for n, see above. The same holds for the hole concentration p q :
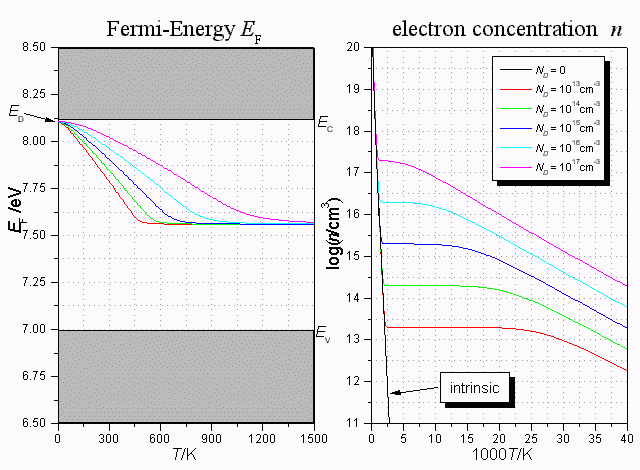 |
| Fermi-Energy EF and electron concentration n in dependence of temperature T for different donator concentrations ND. |